保险专业资源下载网站

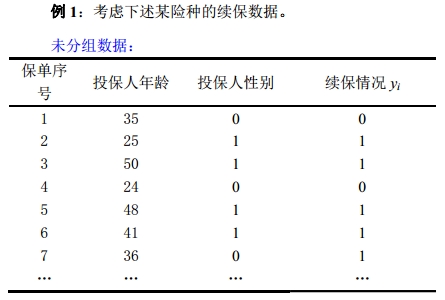
例1：考虑下述某险种的续保数据。
未分组数据：
保单序号
投保人年龄 投保人性别  续保情况yi
1  35  0 0 
2  25  1 1 
3  50  1 1 
4  24  0 0 
5  48  1 1 
6  41  1 1 
7  36  0 1 
…  …  …  … 
分组数据：
投保人年龄
投保人性别
保单总数
续保保单数
小于 35岁 
0 100  60 
1 210  170 
0 120  102 
1 260  230 
35 岁及以上 
0 300  270 
1 100  93 
0 410  370 
1  300  286 
问题：如何分析年龄和性别对续保率影响？ 
假设：第i 组的续保保单数服从二项分布(,) ii Bmπ ，其中mi为该组的保单总数，i π为续保率。
各组续保保单数Yi的概率函数为：
现在考虑n 个保单类别，每个类别的续保次数为
12,,,n YY Y … ，则所有保单类别的联合对数似然函数为 
如果进一步假设续保率是解释变量的函数，即11 () ... ii ipp gx x πβ β =++，（其中g为连接函数），则可以应
用极大似然法（迭代加权最小二乘）求得参数β的估计值。连接函数有多种选择，最常用的是logit连接函数：
注：logit连接可以确保i π的值在（0,1）之间。
其他可供选择的连接函数还有：